Note
Go to the end to download the full example code
1.2. Python-Based Model Definitions
In this tutorial, you will learn how to implement a neurodynamic model with multiple interconnected neural populations using Python only (i.e. without YAML definition files).
Throughout the tutorial, we will make use of the Jansen-Rit neural mass model [1], which describes the dynamic interactions between 3 neural populations via their average firing rates. It has been used to describe the macroscopic, electrophysiological activity within a cortical column. A graphic representation of such a model, placed inside a brain network, can be found in the figure below.
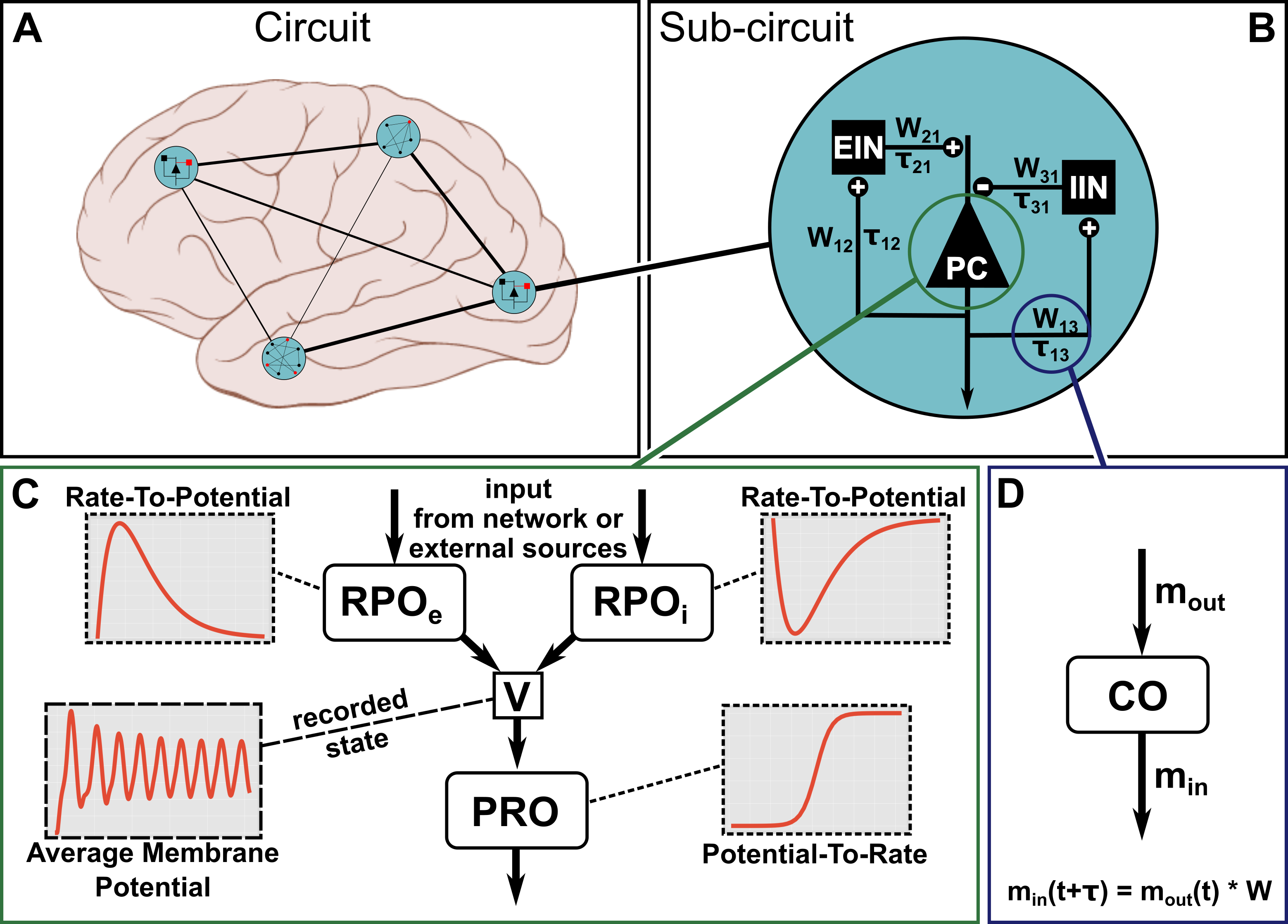
Figure 1
The structure of the full Jansen-Rit model is depicted in Figure 1 B. As visualized for the pyramidal cell population in Figure 1 C, the model can be decomposed into a number of generic mathematical operators that can be used to build the dynamic equations for the Jansen-Rit model. We will use this decomposition to introduce the different possibilities that exist in PyRates to compose the dynamic equations of a neural population from different operators. This will be done for all 3 nodes (i.e. populations), which will then be connected via edges to yield the full Jansen-Rit neural mass model.
1.2.1. References
1.2.1.1. Part 1: Operator Templates
Operator templates are the way to define the governing mathematical equations of a model in PyRates. They are called operators, since the dynamic equations of neural models can often be decomposed into meaningful mathematical operators that can be re-used at multiple instances. By defining such mathematical operators as distinct operator templates in PyRates, these operators just have to be defined once and can then be used to define different parts of a model. We will now go through the 2 major operators that the Jansen-Rit model can be decomposed into.
1.2.2. Operator template for the PRO
First, we will implement the so-called potential-to-rate operator (PRO) used within each neural population of the Jansen-Rit model. As the name suggests, this operator transforms the average membrane potential within a population into an average firing rate. It is defined by the following instantaneous, sigmoidal transform:
In this equation, \(m_{out}\) and \(V\) represent the average firing rate and membrane potential,
respectively, while \(m_{max}\), \(r\) and \(V_{thr}\) are constants defining the maximum firing rate,
firing threshold variance and average firing threshold within the modeled population, respectively.
This operator can be defined via the pyrates.frontend.OperatorTemplate class as follows:
from pyrates.frontend import OperatorTemplate
pro = OperatorTemplate(
name='PRO', path=None,
equations=["m_out = 2.*m_max / (1 + exp(r*(V_th - V)))"],
variables={'m_out': 'output',
'V': 'input',
'V_thr': 6e-3,
'm_max': 2.5,
'r': 560.0},
description="sigmoidal potential-to-rate operator")
In this case, we need the keyword arguments equations and variables to set up an operator (which is identical for
the YAML operator template). As a general rule, every argument that is followed by a list of - <value>
entries in the YAML template also requires a Python list to be passed in the Python call (as it is the case for the
equations argument). Similarly, every argument that is followed by a list of <key>: <value> entries in
the YAML template, requires a Python dictionary to be passed in the Python call (as it is the case for the
variables argument).
1.2.3. Operator template for the RPO
The second important operator in a Jansen-Rit model is the rate-to-potential operator (RPO). It is conceptualized as convolution with an alpha kernel, which can be expressed as a second-order description of the synaptic response dynamics:
In these equations, \(V\) represents the average post-synaptic potential and \(H\) and \(\tau\) are the
efficacy and the time-scale of the synapse, respectively.
A OperatorTemplate instance for the RPO can be created as shown below:
rpo_e = OperatorTemplate(
name='RPO_e', path=None,
equations=['d/dt * V = I',
'd/dt * I = H/tau * m_in - 2 * I/tau - V/tau^2'],
variables={'V': 'output',
'I': 'variable',
'm_in': 'input',
'tau': 0.01,
'H': 0.00325},
description="excitatory rate-to-potential operator")
This is an example of an operator with multiple equations, which are provided as a list of strings. The operator takes a firing rate \(m_{in}\) as input and returns a membrane potential \(V\) as an output. The unit response of that operator is depicted in Figure 1 C. We use the sub-script e to denote that this operator defines the synaptic response dynamic for an excitatory synapse.
1.2.3.1. Part 2: Node Templates
Node templates are what is used in PyRates to define the dynamic equations of a network node (e.g. a neural population) via a hierarchy of operators, such as the ones defined above. Using the two operator templates defined above (PRO and RPO), each population of the Jansen-Rit model can be defined. As shown in Figure 1 B, there exist 3 of those: pyramidal cells (PCs), excitatory interneurons (EINs) and inhibitory interneurons (IINs). We will now define separate node templates for each population.
1.2.4. Node template for the EIN population
As can be seen in in Figure 1 B, the EIN population receives its only (excitatory) input from the PC population.
To model the dynamic changes in the membrane potential that are caused by the firing rate input from the PC
population, the RPO_e operator is used. Furthermore, the EIN population projects back to the PC population
via an excitatory synapse. To receive the average firing rate of the EIN population that is required to implement this
projection, the PRO operator has to be applied to the output of the RPO operator. This provides the operator hierarchy
that governs the role of the EIN population in the Jansen-Rit model. A NodeTemplate instance of this
population can be created as follows:
from pyrates.frontend import NodeTemplate
ein = NodeTemplate(name="EIN", path=None, operators=[pro, rpo_e])
As can be seen above, nodes are defined via a list of operators. Operator hierarchies are automatically derived from
the input and output variables of each operator. Thus, the sequence in which the operators are placed
inside the node template does not matter. However, circular dependencies between the operator inputs and outputs
should be prevented (PyRates throws an error if such circularities are detected). Hence, an output variable on one
operator, that should connect to the input variable of another operator, needs to have the same name as this input
variable.
1.2.5. Node template for the IIN population
As can be seen in Figure 1 B, the IIN population shows an identical connectivity to the PC population as the EIN population. Thus, it expresses an identical operator structure. The only difference between EIN and IIN population is how their projections back to the PC population affect the PC membrane potential, which is excitatory and inhibitory, respectively. Hence, we will define the IIN population template equivalently as:
iin = NodeTemplate(name="IIN", path=None, operators=[pro, rpo_e])
1.2.6. Node template for the PC population
Now, the center piece of the Jansen-Rit model is the PC population, which receives input from both the EIN and the IIN
population. Their synapses have opposing influences on its membrane potential and need to be implemented via two
separate operators that govern the excitatory and inhibitory synaptic dynamics of the EIN to PC and IIN to PC
projections, respectively. However, the operator for the inhibitory synapse will differ from the rpo_e
operator only in the constant values for \(H\) and \(\tau\), i.e. it will have a different strength and
different decay rate. Since the governing equations will be equal, we can use the rpo_e operator and simply
update the two constants, to receive the rpo_i operator:
from copy import deepcopy
rpo_i = deepcopy(rpo_e).update_template(
name='RPO_i', path=None, variables={'H': -0.022, 'tau': 0.02}
)
pc = NodeTemplate(name="PC", path=None, operators=[pro, rpo_e, rpo_i])
Since both the rpo_e and rpo_i operators express an output variable \(V\) and the PRO
operator requires \(V\) as an input, PyRates will detect that there are multiple outputs mapping to a single
input variable. In such a case, a sum will be calculated over all output variables first, which is then provided as
input variable to the respective operator. In this specific example, the input \(m_{in}\) of the PRO operator on
the PC population will be calculated as \(m_{in} = V_e + V_i\) where \(V_e\) and \(V_i\) refer to the
output variables of the rpo_e and rpo_i operators.
1.2.6.1. Part 3: Edge Templates
Edge templates allow to define the dynamic equations for projections between nodes. For example, they could be used to
model axonal delay distributions via a convolution with a delay distribution function. For this purpose, PyRates
provides the EdgeTemplate base template. It follows exactly the same structure as a
NodeTemplate, i.e. it is defined via a base and a colletion of operators. Since the Jansen-Rit
model uses very simple, linear projection operations (see the coupling operator CO in Figure 1 D), no edge
templates are required for this model. A detailed tutorial for how to implement different forms of edge operations
such as delays, convolutions etc., will be provided by the edge definitions example in this gallery.
1.2.6.2. Part 4: Circuit Templates
A circuit template is what is used in PyRates to combine a set of nodes and edges to a full network model.
1.2.7. A circuit template for the Jansen-Rit model
In the case of the Jansen-Rit model, this translates to connecting the PC, EIN and IIN populations via simple, linear
edges that can be set up within the CircuitTemplate as follows:
from pyrates.frontend import CircuitTemplate
jrc = CircuitTemplate(
name="JRC", nodes={'PC': pc, 'EIN': ein, 'IIN': iin},
edges=[("PC/PRO/m_out", "IIN/RPO_e/m_in", None, {'weight': 33.75}),
("PC/PRO/m_out", "EIN/RPO_e/m_in", None, {'weight': 135.}),
("EIN/PRO/m_out", "PC/RPO_e/m_in", None, {'weight': 108.}),
("IIN/PRO/m_out", "PC/RPO_i/m_in", None, {'weight': 33.75})],
path=None)
A circuit template requires the definition of 2 fields: nodes and edges.
nodescan either be a list of all nodes that this circuit is composed of
or a dictionary where the dictionary keys assign names to the nodes in the network
edgesif no edges exist in circuit, this field can be skipped
else, edges are provided as a list and are defined by tuples with four entries:
The source variable (PC/PRO/m_out refers to variable m_out in operator PRO of node PC)
The target variable
An edge template with additional operators (here, null means that no particular edge template is used).
A dictionary of variables and values that are specific to this edge.
more complex syntax can be used within the four entries to define more complex edges. A tutorial on how to use these will be provided by the edge definitions example in this gallery.
This concludes the YAML-based definition of the Jansen-Rit model in PyRates. To learn how to use this model definition to perform numerical simulations, check out the other examples in this gallery.